최근 SCC에 대해 공부하면서 SCC를 구하는 알고리즘은 대표적으로 지난번 공부한 타잔 알고리즘과 코사라주 알고리즘이 있다는 것을 알게 되었습니다.
절대 타잔 알고리즘이 복잡해서가 아니고, 순수하게 학문적인 호기심이 들어서 코사라주 알고리즘을 공부해 보기로 하였습니다.
그럼 아래 그래프의 SCC를 코사라주 알고리즘을 통해 구해보도록 하겠습니다.

우선 DFS의 진행 순서를 생각해 보면 1, 2, 3, 4, 5 입니다. 그럼 함수가 종료되는 (탐색이 끝난 노드?) 순서를 생각해보면 4, 3, 5, 2, 1 이렇게 되겠네요.
여기서 주목해야 할 부분은 2입니다. 위 탐색에서 2번 노드에서 갈 수 있는 노드들은 모두 2번 노드보다 빨리 함수가 종료되게 됩니다. (4, 3, 5 노드)
이제 역방향 그래프가 필요합니다.
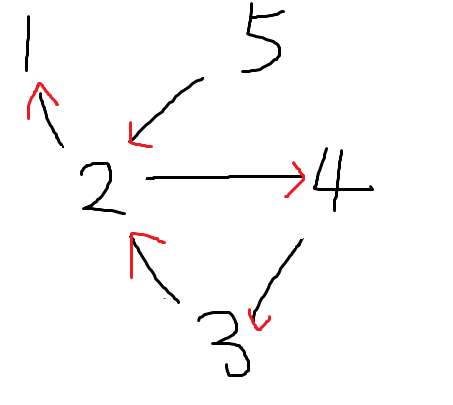
현재 2번 노드에서 갈 수 있는 노드는 3, 4, 5번 노드입니다. 하지만 위 역방향 그래프에서 2번 노드에서 갈 수 있는 노드는 3, 4, 1번 노드입니다.
3, 4번 노드는 정방향과 역방향에서 모두 2번 노드에 도달이 가능합니다. 이는 3, 4 또한 2번 노드를 통해 이동이 가능하다는 것을 의미합니다. (3 > 2 > 4 , 4 > 2 > 3) 이는 SCC의 정의와 같습니다.
위의 과정을 이용하는 것이 코사라주 알고리즘입니다.
1. 정방향 그래프를 DFS를 통한 탐색이 종료되는 순서대로 stack에 넣어준다.
2. stack에서 하나씩 pop 하며 역방향 그래프에서 DFS를 수행한다.
3. 2번을 수행하며 방문한 점들을 하나의 SCC로 만든다.
타잔 알고리즘보다는 구현이 쉬운 알고리즘인 것 같습니다. 두 알고리즘의 시간복잡도 또한 DFS의 시간복잡도인 O(V+E)로 동일합니다.
'어차피 공부는 해야한다. > 알고리즘' 카테고리의 다른 글
| TSP(외판원의 순회) 알고리즘 (0) | 2024.10.24 |
|---|---|
| 밸만 포드 알고리즘과 다이젝스트라 알고리즘 (2) | 2024.10.15 |
| [Graph] SCC 알고리즘 - 타잔 알고리즘, 백준 2150번 (0) | 2024.07.31 |


